Contoh Soal Ulangan Relasi dan Fungsi Beserta Jawabannya.
1. Pada pemetaan bayangan dari 2 adalah …
a. 3 b. 8 c. 9 d. 27
Pembahasan :
f(x) = 4x - 5
f(2) = 4(2) - 5
f(2) = 8 - 5 = 3
2. Pada pemetaan maka h(5) adalah …
a. 33 b. 29 c. 21 d. 17
Pembahasan :
h(x) = x^2 + 4
h(5) = 5^2 + 4
h(5) = 25 + 4 = 29
3. Pada pemetaan f : 5 – x, jika daerah asalnya {-3, -2, -1, 0. 1, 2, 3, 4}, maka daerah hasilnya adalah …
a. {–1, –2, –3, –4, –5, –6, –7, –8} c. {1, 2, 3, 4, 5, 6, 7, 8}
b. {–2, –3, –4, –5, –6, –7, –8, –9} d. {2, 3, 4, 5, 6, 7, 8, 9}
Pembahasan :
f(-3) = 5 - (-3) = 8 f(1) = 5 - 1 = 4
f(-2) = 5 - (-2) = 7 f(2) = 5 - 2 = 3
f(-1) = 5 - (-1) = 6 f(3) = 5 - 3 = 2
f(0) = 5 - 0 = 5 f(4) = 5 - 4 = 1
Daerah Hasilnya = {1, 2, 3, 4, 5, 6, 7, 8}
4. Pada pemetaan jika daerah asalnya {x | x < 5, x Î bilangan asli }, maka daerah hasilnya adalah …
a. {–4, –8, –12, –16, –20} c. {4, 8, 12, 16, 20}
b. {–8, –12, –16, –20, – 22} d. {8, 12, 16, 20, 22}
Pembahasan :
x = {1, 2, 3, 4, 5}
f(1) = 4(1) = 4 f(4) = 4(4) = 16
f(2) = 4(2) = 8 f(5) = 4(5) = 20
f(3) = 4(3) = 12
daerah hasilnya = {4, 8, 12, 16, 20}
5. Pada pemetaan jika daerah asalnya x Î {2, 3, 4, 5 }, rangenya adalah …
a. {4, 11, 14, 15} c. {6, 11, 14, 17}
b. {6, 11, 14, 15} d. {8, 11, 14, 17}
Pembahasan :
f(2) = 3(2) + 2 = 8 f(4) = 3(4) + 2 = 14
f(3) = 3(3) + 2 = 11 f(5) = 3(5) + 2 = 17
Daerah hasilnya = {8, 11, 14, 17}
6. Fungsi f dinyatakan dengan rumus f(x) = px + q, jika f(0) = –2 dan f(2) = 4, maka nilai p dan q berturut-turut adalah …
a. 2 dan –5 b. – 2 dan 5 c. 2 dan –3 d. –2 dan 3
Pembahasan :
f(0) = -2 → p(0) + q = -2 → q = -2
f(2) = 4
p(2) + q = 4
2p + (-2) = 4
2p - 2 = 4←
2p =4 + 2 p = 6/2 = 3
7. Dari tabel di bawah ini, himpunan pasangan berurutannya adalah ….
a. {(0, -1), (1, 1), (2, 3), (3, 5), (4, 7)}
b. {(0, 1), (1, 1), (2, 3), (3, 5), (4, 7)}
c. {(-1, 1), (1, 1), (3, 2), (5, 3), (7, 4)}
d. {(1, -1), (1, 1), (3, 2), (5, 3), (7, 4)}
Pembahasan :
Himpunan Pasangan berurutannya:
{(0, -1), (1, 1), (2, 3), (3, 5), (4, 7)}
8. Dari tabel fungsi f(x) = 3x – 2, rangenya adalah .....
a. {(2, -8), (-1, -5), (0, -2), (1, 1), (2, 4), (3, 7)}
b. {(2, 8), (-1, 5), (0, -2), (1, 1), (2, 4), (3, 7)}
c. {(-8, -2), (-5, -1), (-2, 0), (1, 1), (4, 2), (7, 3)}
d. {(8, -2), (5, -1), (-2, 0), (1, 1), (4, 2), (7, 3)}
Pembahasan :
Range : {(2, -8), (-1, -5), (0, -2), (1, 1), (2, 4), (3, 7)}
9. Diketahui fungsi f : x ---> ax – 7 dan f(5) = 18, maka nilai a adalah …
a. 5 b. 6 c. 7 d. 8
Pembahasan :
f(5) = 18
5a - 7 = 18
5a = 18 + 7
5a = 25, maka a = 5
10. Diketahui fungsi f : x ---> 3x – 11 dan f(a) = –20, maka nilai a adalah …
a. – 3 b. – 4 c. – 5 d. – 6
Pembahasan :
f(a) = -20
3a - 11 = -20
3a = -20 + 11 → 3a = -9 → a = -3
11. Pada pemetaan f : x ---> 3x + 2, jika f :(a )→ 38, maka nilai a adalah …
a. 18 b. 16 c. 12 d. 10
Pembahasan :
f(a) = 38
3a + 2 = 38
3a = 38 - 2
3a = 36 ---> a = 12
12. Diketahui fungsi , jika f( a) ---> 4, maka nilai a adalah …
a. 4 b. 5 c. 6 d. 7
Pembahasan :
<---> x + 3 = 2.4
<---> x + 3 = 8
<---> x = 8 - 3 = 5
13. Diketahui fungsi , jika f(a) = 10, maka nilai a adalah …
a. 22 b. 21 c. 20 d. 19
Pembahasan :
<---> 2a - 12 = 3.10
<---> 2a = 30 + 12
<---> 2a = 42 ----> a = 21
14. Diketahui fungsi f(x) = ax – b, sedangkan f(3) = 4 dan f(–5) = –28, maka nilai a dan b berturut-turut adalah …
a. –3 dan 8 b. 3 dan – 8 c. 4 dan 8 d. 4 dan – 8
Pembahasan :
f(3) = 4 f(-5) = -28
3a - b = 4 .....1) -5a - b = -28 .....2)
Eliminasi b dari pers. 1 dan 2
3a - b = 4
5a + b = 28
________________ +
8a = 32
a = 4
Substitusikan a = 4 ke persamaan 1) :
3(4) - b = 4
12 - b = 4
- b = 4 - 12 ---> b = 8
15. Fungsi f dinyatakan dengan rumus f(x) = ax + b, jika f(2) = 13 dan f(5) = 22, maka nilai a dan b berturut-turut adalah …
a. –4 dan 5 b. 4 dan – 5 c. 3 dan 7 d. 3 dan – 7
Pembahasan :
f(2) = 13 f(5) = 22
2a + b = 13 ..... 1) 5a + b = 22 .... 2)
Eliminasi b dari persamaan 1 dan 2
2a + b = 13
-5a - b = -22
_________________ +
-3a = -9
a = 3
Substitusikan a = 3 ke persamaan 1) :
2(3) + b = 13
6 + b = 13 ----> b = 13 - 6 = 7
16. Fungsi f dinyatakan dengan rumus h(x) = px + q, jika h(–6) = 32 dan h(4) = –8, maka nilai p dan q berturut-turut adalah …
a. –2 dan 9 b. 2 dan – 8 c. 6 dan –4 d. –4 dan 8
Pembahasan :
h(-6) = 32 h(4) = -8
-6p + q = 32 ..... 1) 4p + q = -8 .... 2)
Eliminasi b dari persamaan 1 dan 2
-6p + q = 32
-4p - q = 8
_________________ +
-10p = 40
p = -4
Substitusikan p = -4 ke persamaan 1) :
-6(-4) + q = 32
24 + q = 32 ----> q = 32 - 24 = 8
17. Diketahui fungsi f(x) = ax – b, sedangkan f(3) = 7 dan f(–5) = –25, maka rumus fungsi f(x) adalah …
a. f(x) = 3x +5 b. f(x) = 3x – 5 c. f(x) = 4x + 5 d. f(x) = 4x – 5
Pembahasan :
f(3) = 7 f(-5) = -25
3a - b = 7 ..... 1) -5a - b = -25 .... 2)
Eliminasi b dari persamaan 1 dan 2
3a - b = 7
5a + b = 25
_________________ +
8a = 32
a = 4
Substitusikan a = 4 ke persamaan 1) :
3(4) - b = 7
12 - b = 7 ----> -b = 7 - 12 = 5
Rumus fungsi f(x) = 4x - 5
18. Fungsi f dinyatakan dengan rumus f(x) = ax + b, jika f(2) = 13 dan f(5) = 22, maka rumus fungsi f(x) adalah …
a. f(x) = 3x + 7 b. f(x) = 3x – 7 c. f(x) = 2x + 5 d. f(x) = 2x – 5
Pembahasan :
f(2) = 13 f(5) = 22
2a + b = 13 ..... 1) 5a + b = 22 .... 2)
Eliminasi b dari persamaan 1 dan 2
2a + b = 13
-5a - b = -22
_________________ +
-3a = -9
a = 3
Substitusikan a = 3 ke persamaan 1) :
2(3) + b = 13
6 + b = 13 ----> b = 13 - 6 = 7
Rumus funfsi f(x) = 3x + 7
19. Fungsi f dinyatakan dengan rumus h(x) = px + q, jika h(–6) = 32 dan h(4) = –8, maka rumus fungsi h(x) adalah …
a. f(x) = – 5x + 8 b. f(x) = –5x – 8 c. f(x) = – 4x + 8 d. f(x) = –4x – 8
Pembahasan :
h(-6) = 32 h(4) = -8
-6p + q = 32 ..... 1) 4p + q = -8 .... 2)
Eliminasi b dari persamaan 1 dan 2
-6p + q = 32
-4p - q = 8
_________________ +
-10p = 40
p = -4
Substitusikan p = -4 ke persamaan 1) :
-6(-4) + q = 32
24 + q = 32
q = 32 - 24 = 8
Jadi rumus fungsi f(x) = -4x + 8
20. Nilai a, b dan c dari tabel f(x) = 2x + 2, berturut-turut adalah …
a. [2, 4, 6} b. [2, 6, 8} c. [4, 6, 8} d. [4, 8, 10}
Pembahasan :
f(0) = 2(0) + 2 → a = 2
f(2) = 2(2) + 2→ b = 6
f(3) = 2(3) + 2
c = 8 -----> maka nilai a, b, dan c = [2, 6, 8]
21. Diketahui A = {1, 2, 3, 4} dan B = {a, b, c, d}
a. Tulislah himpuanan pasangan berurutan yang menunjukkan korespondensi satu-satu dari A ke B !
b. Berapakan banyak koresponden satu-satu dari A ke B ?
Pembahasan :
a. {(1, a), (2, b), (3, c), (4, d)} b. (1 x 2 x 3 x 4) = 24
22. Fungsi f dinyatakan dengan rumus f(x) = ax + b, jika f(2) = 13 dan f(5) = 22.
Tentukan :
a. Nilai a dan b
b. rumus fungsi f(x)
c. Tentukan nilai f(10)
Pembahasan :
a. f(x) = ax + b, jika f(2) = 13 maka :
f(2) = 2a + b → 2a + b = 13 … 1) f(x) = ax + b, jika f(5) = 22 maka :
f(5) = 5a + b → 5a + b = 22 … 2)
Eliminasi b dari pers. 1) dan 2)
2a + b = 13
5a + b = 22 –
−3a = −9→a = 3
Substitusikan a = 3 ke pers. 1)
2a + b = 13 →2(3) + b = 13
6 + b = 13 →b = 7
→ b. Substitusikan a = 3 dan b = 7 ke fungsi f,
maka rumus fungsi menjadi : f(x) = 3x + 7
c. f(x) = 3x + 7, jika f(10) maka :
f(10) = 3(10) + 7
= 30 + 7 = 37
23. Fungsi f dinyatakan dg rumus h(x) = px + q, jika h(–6) = 32 dan h(4) = –8,
Tentukan :
a. Nilai p dan q b. rumus fungsi h(x) c. nilai h(−2)
Pembahasan :
a. h(x) = px + q, jika h(−6) = 32 maka :
h(−6) = −6p + q →−6p + q = 32 … 1) h(x) = px + q, jika h(4) = −8 maka :
h(4) = 4p + q →4p + q = −8 … 2)
Eliminasi q dari pers. 1) dan 2)
−6p + q = 32
4p + q = −8 –
−10p = 40 →p = −4
Substitusikan p = −4 ke pers. 1)
−6p + q = 32 → −6(−4) + q = 32
→ 24 + q = 32→q = 32 – 24 = 8
b. Substitusikan p = −4 dan q = 8 ke fungsi h, maka rumus fungsi menjadi : h(x) = −4x + 8
c. h(x) = −4x + 8, jika h(−2) maka :
h(−2) = 3(−2) + 8 = −6 + 8 = 2
b. Substitusikan p = −4 dan q = 8 ke fungsi h, maka rumus fungsi menjadi : h(x) = −4x + 8
c. h(x) = −4x + 8, jika h(−2) maka :
h(−2) = 3(−2) + 8 = −6 + 8 = 2
24
25.Dikelas 8 SMP belajar matematika terdapat 4 orang siswa yang lebih menyukai pelajaran tertentu. berikut ke-4 anak tersebut :
• Buyung menyukai pelajaran IPS dan Kesenian
• Doni menyukai pelajaran ketrampilan dan olah raga
• Vita menyukai pelajaran IPA, dan
• Putri lebih menyukai pelajaran matematika dan bahasa ingris
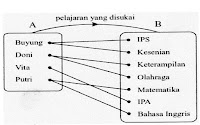
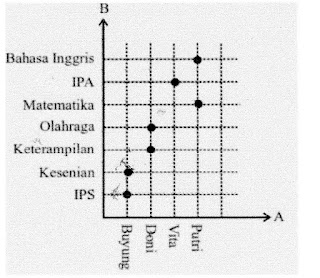
Buatlah relasi dari soal diatas dan disajikan menggunakan diagram panah, diagram cartesius, dan himpunan pasangan berurutan.
Jawab :
Untuk mempermudah menjawab persoalan diatas gunakanlah permisalan seperti : Himpunan A = {Buyung, Doni, Vita, Putri}, Himpunan B = {IPS, kesenian, keterampilan, olahraga, matematika, IPA, bahasa Inggris}, dan “pelajaran yang disukai” adalah relasi yang menghubungkan himpunan A ke B.
Diagram panah
Diagram Cartesius
Himpunan pasangan berurutan
Himpunan pasangan berurutan dari soal diatas adalah {(Buyung, IPS), (Buyung, kesenian), (Doni, keterampilan), (Doni, olahraga), (Vita, IPA), (Putri, matematika), (Putri, bahasa Inggris)}
26. Dari tabel fungsi f(x) = 3x – 2, rangenya adalah .....
a. {(2, -8), (-1, -5), (0, -2), (1, 1), (2, 4), (3, 7)}
b. {(2, 8), (-1, 5), (0, -2), (1, 1), (2, 4), (3, 7)}
c. {(-8, -2), (-5, -1), (-2, 0), (1, 1), (4, 2), (7, 3)}
d. {(8, -2), (5, -1), (-2, 0), (1, 1), (4, 2), (7, 3)}
Pembahasan :
Range : {(2, -8), (-1, -5), (0, -2), (1, 1), (2, 4), (3, 7)}
27. Diketahui fungsi f : x ---> ax – 7 dan f(5) = 18, maka nilai a adalah …
a. 5 b. 6 c. 7 d. 8
Pembahasan :
f(5) = 18
5a - 7 = 18
5a = 18 + 7
5a = 25, maka a = 5
28. Diketahui fungsi f : x ---> 3x – 11 dan f(a) = –20, maka nilai a adalah …
a. – 3 b. – 4 c. – 5 d. – 6
Pembahasan :
f(a) = -20
3a - 11 = -20
3a = -20 + 11 →3a = -9 → a = -3
29. Pada pemetaan f : x ---> 3x + 2, jika f :(a )→38, maka nilai a adalah …
a. 18 b. 16 c. 12 d. 10
Pembahasan :
f(a) = 38
3a + 2 = 38
3a = 38 - 2
3a = 36 ---> a = 12
30. Diketahui fungsi , jika f( a) ---> 4, maka nilai a adalah …
a. 4 b. 5 c. 6 d. 7
Pembahasan :
<---> x + 3 = 2.4
<---> x + 3 = 8
<---> x = 8 - 3 = 5






Terima kasih, sangat bermanfaat...
ReplyDeleteMy blog
Terima kasih. Sangat membantu sekali, dan sangat bermanfaat buat saya.
ReplyDeleteTerimkasii sangat membantu sekali
ReplyDeleteTerima kasih,membantu sekalii
ReplyDeleteTerimakasih
ReplyDeleteTHANKS SANGAT MEMBANTU
ReplyDeleteAstaga,Rumus Rumusnya/ bentuk pemetaannya gak Ditulis Mamang Mau Tau gimana? NEBAK Pake Otak Dong
ReplyDeleteYth DearHAMBAاللّٰهِ,
ReplyDeleteI 💖 U 👁️Buka👁️
BisnisDigital:
CheckGoogle
👇🏿Click👇🏿🧐😊👍🏾!
http://bit.ly/aaaabisniscerdas
👍🏾Rekomendasi Peserta Aktif!
Niat u/cari rizki اللّٰهِ, Ingal Inga zikiiir 📿no.1 اللّٰهِ👍Alhamdulillah👌Dahsyaaat LuuuarBiasa🗣️اللّٰهِAkbar🇸🇦🈴lfatihah.. Insya اللّٰهBerkah
http://bit.ly/aaaabisniscerdas
👍🏾
http://bit.ly/aaaabisniscerdas
ReplyDeleteTerima kasih,ini membantu sekali
ReplyDeleteI Like Your Artcile. This Article is Amazing and Easy Tp Understand
ReplyDeleteClick Here